Un beau jour, au siècle dernier, un jeune étudiant s'amusant à feuilleter les livres d'André Chéron sur les finales (Lehr-und Handbuch der Endspiele en 4 volumes, Das SchachArchiv, Hamburg 1955-1970, Tome III page 277) tomba en arrêt devant le diagramme suivant :

A. Crosskill (1864)

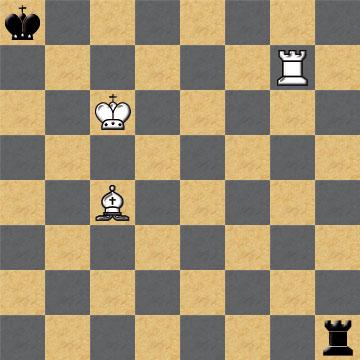
Il était précisé que les Blancs gagnent en 57 coups ! La "solution" suivait, avec peu de commentaires : un excellent défi pour un joueur passionné de recherche, ayant déjà participé au championnat de France... Amère surprise : quoique disposant de tout son temps, allant jusqu'à négliger les cours de mathématiques de la Faculté de Montpellier (avec tous les déchirements que cela suppose), notre étudiant fut incapable de la comprendre. Ou plutôt, d'en comprendre davantage que les quinze derniers coups, lesquels constituent la méthode de Philidor (milieu du XVIIIe siècle) telle qu'il l'avait apprise, quelques années plus tôt, dans le "Bréviaire des Echecs" de X. Tartakower.

Ce fut pour lui un choc, dont la leçon peut se formuler ainsi : à quoi sert d'étudier plus avant la stratégie et la tactique, de s'efforcer de devenir un fort joueur, un champion de France peut-être, si l'on reste désarmé devant une "simple" position de cinq pièces ? Par la suite, ce doute a continué de se manifester en filigrane : notre joueur, devenu plus tard maître international, en a conservé un certain dédain amusé pour les exercices tactiques du milieu de partie, comme pour le travail des ouvertures, activités auxquelles il a pourtant dû sacrifier une grande partie de son temps.

Bien sûr, il est déconseillé au lecteur de partager cette vision des choses. Il faut rétablir dans son esprit l'importance de tous les secteurs du jeu. Qu'il retienne cependant ceci : le degré de complexité de certaines finales au matériel élémentaire dépasse les aptitudes d'un joueur normal, mais aussi, ce qui est moins banal, d'un champion du monde. Je prends en effet le pari suivant : pas un seul joueur de niveau mondial n'est capable (sauf -- et encore -- à se mettre en congé pour des mois et ainsi compromettre sa carrière) de fournir un exposé satisfaisant sur la manière dont deux Fous gagnent contre un Cavalier (sans pions). Ou bien, privé d'ordinateur, de résoudre, parmi cent autres, l'étude suivante : Rb1, Dh5, Ph6 / Ra6, Dh7 : + - où les Blancs réussissent à forcer la promotion de leur pion en 107 coups ! Epargnons-lui tout de même les turbulences de D + C / 2T (gain en 150 coups) et celles de T + F / 2C (pas moins de 223 coups).

Les finales ci-dessus n'intéressent que fort peu le joueur pratique (de compétition ou occasionnel) auquel s'adresse notre livre. Néanmoins, à titre de curiosité, nous donnons ci-après la solution "brute" de l'étude de Crosskill. Quant au "mastodonte" avec Dame et pion contre Dame, sachez simplement que la dernière phase de la solution correspond à la redoutable étude de K. Staleraïtis, analysée en détail au chapitre IV.

Le cas de la finale "Deux Fous contre Cavalier" est fort divertissant. A l'heure actuelle, les programmes spécialisés traitent de façon exhaustive la plupart des finales comportant jusqu'à six unités, Rois inclus. En vérité, ils donnent pour chaque position une suite de coups "idéale" (le gain le plus court si la position est gagnante, la ou les façons d'annuler dans le cas contraire). Mais bien souvent cette suite, qui n'est pas une méthode, est absconse et déroutante ; parfois même (c'est le cas pour 2F / C), il est quasi impossible de la reproduire, ou de l'adapter, dans la pratique. C'est ainsi qu'en tournoi, lorsque cette finale se présente, même si les adversaires arborent plus de 2500 points "Elo", la partie se termine généralement par la nulle, après diverses tentatives épuisant la "règle des cinquante coups". Aussi longtemps qu'une méthode claire et précise démontrant le gain n'aura pas été mise sur pied, certains joueurs persisteront à considérer cette finale comme nulle, arguant que "seul doit être tenu pour acquis ce qui est compréhensible à l'échelle humaine", dans une activité où le réalisme est de rigueur. A l'inverse, d'autres s'inclineront devant ce que l'ordinateur (certains disent le Monstre, d'autres l'Oracle) a décrété, et qui est mathématiquement exact. C'est notamment le cas des compositeurs d'études artistiques, pour qui deux Fous gagnent contre un Cavalier, un point c'est tout : les juges, qui décernent en conséquence prix et mentions dans les concours, seraient bien en peine d'expliquer de quelle façon ! Voir au chapitre X un exemple caractéristique du démantèlement de la "forteresse Kling et Horwitz".

Le joueur pratique, bien heureusement, n'aura pas à connaître de toutes ces subtilités : dans l'immense généralité des positions étudiées ici, la distinction entre le gain et la nulle (entre le coup gagnant et celui qui laisse échapper la victoire, entre le coup annulant et celui qui perd) est entièrement vérifiable, au pire après un certain temps d'analyse. Et quand cette distinction a été comprise, elle l'est pour toujours, sous réserve d'un rafraîchissement de mémoire de temps à autre. C'est ainsi que le lecteur peut structurer ses acquisitions, et donc progresser, ce qui est l'unique propos de cet ouvrage.

Dans une telle perspective, nous avons intégré les précieux enseignements de la Machine, sans toutefois lui consentir un pouvoir trop exorbitant. Sans craindre de faire entorse à ses oukases, nous avons délibérément préféré :

-- à la suite gagnante la plus courte, la suite la plus claire.

-- à la défense la plus longue (résistante en nombre de coups), la meilleure défense (difficile à réfuter).

-- quand plusieurs coups annulent, le plus sûr ou le plus naturel.  

Ce que souhaite le joueur ayant l'avantage matériel en finale, c'est de réaliser le gain. Peu lui importe de jouer dix coups de trop (tant qu'il reste en deçà des cinquante coups autorisés sans prise ni mouvement de pion) pourvu qu'il sache où il va. Il lui faut comprendre, gagner et non battre un record de rapidité. Le texte doit privilégier la ligne de jeu la plus riche, la plus difficile à découvrir par soi-même, quitte à supprimer, ou reléguer entre parenthèses une suite plus automatique. Particulièrement importantes sont les défenses contrecarrées par un coup unique. Si le joueur est en infériorité, il doit aussi connaître ces défenses ingénieuses, pour compliquer la tâche de son adversaire. S'il sait que la position est nulle, il appréciera, parmi les coups possibles, le plus susceptible d'être retenu (on n'a pas toujours le livre sous la main), celui après lequel il risque le moins de se tromper (on ne peut retenir toutes les variantes), parfois aussi le plus actif (pour l'impact psychologique). Il sera sensible à l'expression limpide d'idées-forces, de schémas de base, de forteresses qui l'aideront à se repérer.

Au risque d'enfoncer quelques portes ouvertes, répétons que la Machine est fort utile au joueur d'Echecs, tant qu'elle reste à sa seule place : celle d'un outil. Espérons, à ce propos, que nos lecteurs se tiendront à distance respectable de deux espèces actuellement florissantes : les ordinocrates qui, après avoir audacieusement affirmé que "Dieu est mort", n'ont eu de cesse qu'ils lui aient substitué inconsciemment une pseudodivinité informatique, et les ordinomanes qui à tout instant pressent le bouton, comme d'autres pressent celui de leur téléviseur, sans réfléchir à cet engrenage : somnolence de l'esprit, conformisme, paralysie du sens critique, barbarie...

N'oublions pas également cette évidence que l'ordinateur, quand il joue bien, ne sait pas pourquoi il joue bien : sa virtuosité dans bien des cas (comme l'exemple T + F / T ci-dessus) contraste comiquement avec son hésitation et sa maladresse dès qu'un pion se trouve en septième rangée (et que par suite quatre promotions sont à tout moment envisageables dont trois sont, en général, éliminées instinctivement par le joueur humain). Quoi qu'il en soit, il nous a rendu service, en nous inspirant maintes corrections dans les finales suivantes : T + P / T, D + P / D, D / T + P, C + P / C, F + P / C, T + P / F, T / C, T + F / T, T + C / T, 2F / C, D / 2F, D / 2C etc. Et plus récemment : T + P / T + P, T + P / F + P, T + P / C + P, T + 2P / T, T / F + 2P, T / C + 2P.

Nous ne résistons pas au plaisir d'un exemple immédiat, où la déception de s'être trompé cède vite la place, dans l'esprit de l'auteur, aux délices de l'élégante trouvaille, même s'il n'y est pour rien !